TensorFlow实现单变量线性回归
学习的函数为线性函数 y=2x+1
1
2
3
4
5
6
| import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
|
生成人工数据集
1
2
3
4
5
|
x_data = np.linspace(-1, 1, 100)
y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4
|
array([ 0.79242262, 0.17076445, -1.75374086, 0.63029648, 0.49832921,
1.01813761, -0.84646862, 2.52080763, -1.23238611, 0.72695326])
(100,)
1
2
3
4
|
np.random.randn(*x_data.shape)
|
array([ 0.04595522, -0.48713265, 0.81613236, -0.28143012, -2.33562182,
-1.16727845, 0.45765807, 2.23796561, -1.4812592 , -0.01694532,
1.45073354, 0.60687032, -0.37562084, -1.42192455, -1.7811513 ,
-0.74790579, -0.36840953, -2.24911813, -1.69367504, 0.30364847,
-0.40899234, -0.75483059, -0.40751917, -0.81262476, 0.92751621,
1.63995407, 2.07361553, 0.70979786, 0.74715259, 1.46309548,
1.73844881, 1.46520488, 1.21228341, -0.6346525 , -1.5996985 ,
0.87715281, -0.09383245, -0.05567103, -0.88942073, -1.30095145,
1.40216662, 0.46510099, -1.06503262, 0.39042061, 0.30560017,
0.52184949, 2.23327081, -0.0347021 , -1.27962318, 0.03654264,
-0.64635659, 0.54856784, 0.21054246, 0.34650175, -0.56705117,
0.41367881, -0.51025606, 0.51725935, -0.30100513, -1.11840643,
0.49852362, -0.70609387, 1.4438811 , 0.44295626, 0.46770521,
0.10134479, -0.05935198, -2.38669774, 1.22217056, -0.81391201,
0.95626186, -0.63851056, -0.14312642, -0.22418983, -1.03849524,
-0.17170905, 0.47634618, -0.41417827, -1.26408334, -0.57321556,
0.24981732, 1.14720208, 0.83594396, 0.28740365, -0.9955963 ,
0.90688947, 0.02421074, -0.23998173, 0.91011056, 0.61784475,
0.49961804, -1.15154425, -0.6105164 , -1.70388541, 0.19443738,
0.02824125, 0.93256051, 0.21204332, -0.36794457, 2.1114884 ])
array([-1.02957349, -1.33628031, -0.61056736, 0.52469426, -0.34930813,
-0.44073846, -1.1212876 , 1.47284473, -0.62337224, -1.08070195,
-0.12253009, -0.8077431 , -0.23255622, 1.33515034, -0.44645673,
-0.04978868, -0.36854478, -0.19173957, 0.81967992, 0.53163372,
-0.34161504, -0.93090048, -0.13421699, 0.83259361, -0.01735327,
-0.12765822, -1.80791662, 0.99396898, -1.49112886, -1.28210748,
-0.37570741, 0.03464388, 0.04507816, -0.76374689, -0.31313851,
-0.60698954, -1.80955123, -0.25551774, -0.69379935, 0.41919776,
-0.14520019, 0.9638013 , 0.69622199, 0.89940546, 1.20837807,
0.6932537 , -0.16636061, 1.35311311, -0.92862651, -0.03547249,
0.85964595, -0.28749661, 0.71494995, -0.8034526 , -0.54048196,
0.54617743, 0.71188926, 1.19715449, -0.07006703, 0.29822712,
0.62619261, 0.46743206, -1.30262143, -0.57008965, 1.44295001,
-1.24399513, 0.62888033, -0.42559213, 1.00320956, -0.77817761,
0.04894463, -2.02640189, -0.04193635, 1.07454278, -1.5008594 ,
1.18574443, -0.71508124, -0.05123853, -2.77458336, 1.07862813,
-0.87568592, -0.53810932, -1.2782157 , -0.99276945, 1.14342789,
-0.5090726 , 0.89500094, -0.17620337, 0.34608347, -0.50631013,
0.42716402, 2.58856959, 0.65289301, 0.50583979, -0.47595083,
1.01090874, 1.35920097, -1.70208997, -1.38033223, 2.10177668])
1
2
|
y_data = 2 * x_data + 1.0 + np.random.randn(100) * 0.4
|
matplotlib画出生成结果
1
2
|
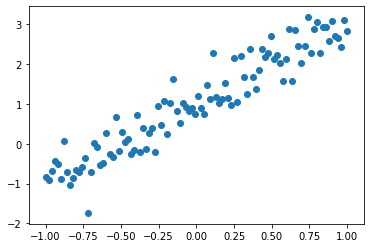
plt.scatter(x_data, y_data)
|
<matplotlib.collections.PathCollection at 0x22c32a84c18>
![png]()
1
2
3
|
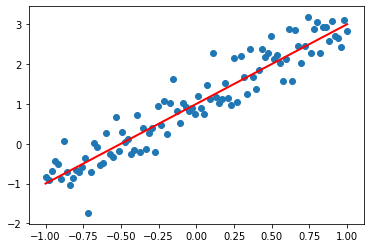
plt.scatter(x_data, y_data)
plt.plot(x_data, 1.0 + 2 * x_data, color = 'red', linewidth=2)
|
[<matplotlib.lines.Line2D at 0x22c32b14f28>]
![png]()
构建模型
定义x和y的占位符
1
2
3
|
x = tf.placeholder("float", name = "x")
y = tf.placeholder("float", name = "y")
|
构建回归模型
1
2
3
4
5
|
def model(x, w, b):
return tf.multiply(x, w) + b
|
创建变量
- 变量声明函数使tf.Variable
- 变量作用是保存和更新模型参数
- 变量的初始化可以是随机数、常数,或者其他变量的初始值计算得到
1
2
3
4
5
6
|
w = tf.Variable(1.0, name = "w0")
b = tf.Variable(0.0, name = "b0")
|
训练模型
设置训练参数
关于学习率(learning_rate)的设置
- 学习率作用:控制参数更新的幅度
- 学习率设置过大:可能导致参数在极值附件来回摇摆,无法保证收敛
- 学习率设置国小:虽然能保证收敛,但是优化速度大大降低,需要迭代次数更多次数才能达到比较理想的优化效果
定义损失函数
- 损失函数用于描述预测值和真实值之间的误差,从而指导模型收敛方向
- 常见损失函数:均方差(Mean Square Errir,MSE)和交叉熵(cross-entropy)
$ L_2 损失函数 $
1
2
3
|
loss_function = tf.reduce_mean(tf.square(y-pred))
|
定义优化器
- 定义优化器Optimizer,初始化一个GradientDescentOptimizer
- 设置学习率和优化目标:最小化损失
1
2
3
4
5
|
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)
|
创建会话
1
2
3
4
|
init = tf.global_variables_initializer()
sess.run(init)
|
迭代训练
模型训练阶段设置迭代轮次,每次通过将样本逐个输入模型,进行梯度下降优化操作,每轮迭代后绘制出模型曲线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
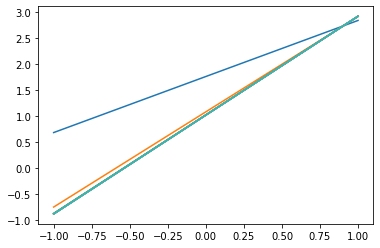
step = 0
loss_list = []
for epoch in range(train_epochs):
for xs, ys in zip(x_data, y_data):
_, loss = sess.run([optimizer, loss_function], feed_dict={x:xs, y:ys})
loss_list.append(loss)
step = step+1
if step % display_step == 0:
print("Train Epoch:",'%02d' % (epoch+1), "Step:%03d" % (step),"loss=","{:.9f}".format(loss))
b0temp = b.eval(session=sess)
w0temp = w.eval(session=sess)
plt.plot (x_data, w0temp * x_data + b0temp)
|
Train Epoch: 01 Step:010 loss= 0.053888980
Train Epoch: 01 Step:020 loss= 0.000218245
Train Epoch: 01 Step:030 loss= 0.019443041
Train Epoch: 01 Step:040 loss= 0.589532554
Train Epoch: 01 Step:050 loss= 0.000989183
Train Epoch: 01 Step:060 loss= 0.142488658
Train Epoch: 01 Step:070 loss= 0.046271212
Train Epoch: 01 Step:080 loss= 0.008660123
Train Epoch: 01 Step:090 loss= 0.241159379
Train Epoch: 01 Step:100 loss= 0.000514947
Train Epoch: 02 Step:110 loss= 0.317517459
Train Epoch: 02 Step:120 loss= 0.032397330
Train Epoch: 02 Step:130 loss= 0.093368128
Train Epoch: 02 Step:140 loss= 0.332103789
Train Epoch: 02 Step:150 loss= 0.060521714
Train Epoch: 02 Step:160 loss= 0.024084859
Train Epoch: 02 Step:170 loss= 0.178793266
Train Epoch: 02 Step:180 loss= 0.006461896
Train Epoch: 02 Step:190 loss= 0.129687995
Train Epoch: 02 Step:200 loss= 0.013333416
Train Epoch: 03 Step:210 loss= 0.129900724
Train Epoch: 03 Step:220 loss= 0.023582600
Train Epoch: 03 Step:230 loss= 0.096030191
Train Epoch: 03 Step:240 loss= 0.317024857
Train Epoch: 03 Step:250 loss= 0.069221057
Train Epoch: 03 Step:260 loss= 0.018716505
Train Epoch: 03 Step:270 loss= 0.193809599
Train Epoch: 03 Step:280 loss= 0.009021518
Train Epoch: 03 Step:290 loss= 0.121858403
Train Epoch: 03 Step:300 loss= 0.015201909
Train Epoch: 04 Step:310 loss= 0.117845014
Train Epoch: 04 Step:320 loss= 0.022902815
Train Epoch: 04 Step:330 loss= 0.096256405
Train Epoch: 04 Step:340 loss= 0.315768689
Train Epoch: 04 Step:350 loss= 0.069981642
Train Epoch: 04 Step:360 loss= 0.018294554
Train Epoch: 04 Step:370 loss= 0.195104137
Train Epoch: 04 Step:380 loss= 0.009256961
Train Epoch: 04 Step:390 loss= 0.121209100
Train Epoch: 04 Step:400 loss= 0.015365199
Train Epoch: 05 Step:410 loss= 0.116854727
Train Epoch: 05 Step:420 loss= 0.022845931
Train Epoch: 05 Step:430 loss= 0.096275523
Train Epoch: 05 Step:440 loss= 0.315662980
Train Epoch: 05 Step:450 loss= 0.070045985
Train Epoch: 05 Step:460 loss= 0.018259227
Train Epoch: 05 Step:470 loss= 0.195213363
Train Epoch: 05 Step:480 loss= 0.009276883
Train Epoch: 05 Step:490 loss= 0.121154651
Train Epoch: 05 Step:500 loss= 0.015378974
Train Epoch: 06 Step:510 loss= 0.116771445
Train Epoch: 06 Step:520 loss= 0.022841139
Train Epoch: 06 Step:530 loss= 0.096277155
Train Epoch: 06 Step:540 loss= 0.315654010
Train Epoch: 06 Step:550 loss= 0.070051350
Train Epoch: 06 Step:560 loss= 0.018256264
Train Epoch: 06 Step:570 loss= 0.195222735
Train Epoch: 06 Step:580 loss= 0.009278628
Train Epoch: 06 Step:590 loss= 0.121149838
Train Epoch: 06 Step:600 loss= 0.015380217
Train Epoch: 07 Step:610 loss= 0.116764441
Train Epoch: 07 Step:620 loss= 0.022840742
Train Epoch: 07 Step:630 loss= 0.096277267
Train Epoch: 07 Step:640 loss= 0.315653324
Train Epoch: 07 Step:650 loss= 0.070051797
Train Epoch: 07 Step:660 loss= 0.018256038
Train Epoch: 07 Step:670 loss= 0.195223376
Train Epoch: 07 Step:680 loss= 0.009278720
Train Epoch: 07 Step:690 loss= 0.121149674
Train Epoch: 07 Step:700 loss= 0.015380275
Train Epoch: 08 Step:710 loss= 0.116763875
Train Epoch: 08 Step:720 loss= 0.022840688
Train Epoch: 08 Step:730 loss= 0.096277334
Train Epoch: 08 Step:740 loss= 0.315653145
Train Epoch: 08 Step:750 loss= 0.070051856
Train Epoch: 08 Step:760 loss= 0.018255942
Train Epoch: 08 Step:770 loss= 0.195223376
Train Epoch: 08 Step:780 loss= 0.009278720
Train Epoch: 08 Step:790 loss= 0.121149503
Train Epoch: 08 Step:800 loss= 0.015380275
Train Epoch: 09 Step:810 loss= 0.116763793
Train Epoch: 09 Step:820 loss= 0.022840688
Train Epoch: 09 Step:830 loss= 0.096277334
Train Epoch: 09 Step:840 loss= 0.315653145
Train Epoch: 09 Step:850 loss= 0.070051923
Train Epoch: 09 Step:860 loss= 0.018255910
Train Epoch: 09 Step:870 loss= 0.195223585
Train Epoch: 09 Step:880 loss= 0.009278766
Train Epoch: 09 Step:890 loss= 0.121149339
Train Epoch: 09 Step:900 loss= 0.015380275
Train Epoch: 10 Step:910 loss= 0.116763711
Train Epoch: 10 Step:920 loss= 0.022840671
Train Epoch: 10 Step:930 loss= 0.096277304
Train Epoch: 10 Step:940 loss= 0.315653145
Train Epoch: 10 Step:950 loss= 0.070051856
Train Epoch: 10 Step:960 loss= 0.018255973
Train Epoch: 10 Step:970 loss= 0.195223376
Train Epoch: 10 Step:980 loss= 0.009278720
Train Epoch: 10 Step:990 loss= 0.121149503
Train Epoch: 10 Step:1000 loss= 0.015380275
![png]()
[<matplotlib.lines.Line2D at 0x22c32cef9e8>]
![png]()
1
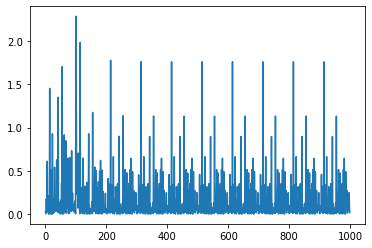
| plt.plot(loss_list,'r+')
|
[<matplotlib.lines.Line2D at 0x22c32d45ba8>]
![png]()
1
| [x for x in loss_list if x>1]
|
[1.4533501,
1.3507473,
1.7046989,
2.2887022,
1.7251762,
1.9852284,
1.1750387,
1.7792182,
1.1360258,
1.7623546,
1.132765,
1.7609351,
1.1324903,
1.7608157,
1.1324672,
1.7608054,
1.1324654,
1.7608048,
1.1324649,
1.7608048,
1.1324646,
1.7608044,
1.1324649]
1
2
3
|
print("w:", sess.run(w))
print("b:", sess.run(b))
|
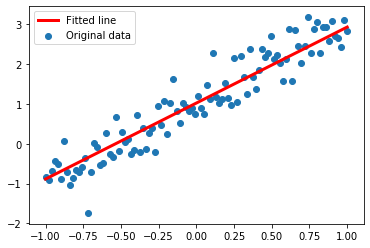
w: 1.9070293
b: 1.0205086
1
2
3
4
|
plt.scatter(x_data, y_data, label="Original data")
plt.plot(x_data,x_data * sess.run(w)+sess.run(b),label = "Fitted line", color = 'r',linewidth = 3)
plt.legend(loc = 2)
|
<matplotlib.legend.Legend at 0x22c32da9c50>
![png]()
1
2
| for xs,ys in zip(x_data, y_data):
print(xs, ys)
|
-1.0 -0.8296403329862183
-0.9797979797979798 -0.907915867983997
-0.9595959595959596 -0.6940069139116888
-0.9393939393939394 -0.44008198904613316
-0.9191919191919192 -0.518056298082633
-0.898989898989899 -0.8872131046936622
-0.8787878787878788 0.06789250806751634
-0.8585858585858586 -0.7121223166059172
-0.8383838383838383 -1.0266771956105798
-0.8181818181818181 -0.8591953886106469
-0.797979797979798 -0.6488803761421159
-0.7777777777777778 -0.7072455496370039
-0.7575757575757576 -0.5902689976300266
-0.7373737373737373 -0.3485610146594407
-0.7171717171717171 -1.7479096133940975
-0.696969696969697 -0.7054166950286986
-0.6767676767676767 0.02660252968277821
-0.6565656565656566 -0.0879307925836007
-0.6363636363636364 -0.5449888988689496
-0.6161616161616161 -0.4821245885002341
-0.5959595959595959 0.26427918331828665
-0.5757575757575757 -0.2506067288023764
-0.5555555555555556 -0.3231932210702846
-0.5353535353535352 0.6715786910122715
-0.5151515151515151 -0.17825188097185915
-0.4949494949494949 0.2837997365730506
-0.4747474747474747 0.03223693168166275
-0.4545454545454545 0.11122375083990527
-0.43434343434343425 -0.24757709110216308
-0.41414141414141414 -0.15907779562657415
-0.3939393939393939 0.7153506547917942
-0.3737373737373737 -0.20303085077192035
-0.3535353535353535 0.4038733399023537
-0.33333333333333326 -0.14444505243328032
-0.31313131313131304 0.2775626397745727
-0.2929292929292928 0.39925810781510473
-0.2727272727272727 -0.19732590501344383
-0.2525252525252525 0.9488948450886014
-0.23232323232323226 0.46183376274541277
-0.21212121212121204 1.0616526671192374
-0.19191919191919182 0.24245017816545178
-0.1717171717171716 1.0213106217668546
-0.1515151515151515 1.6306657350096654
-0.13131313131313127 0.8239865196438662
-0.11111111111111105 0.5189503868361454
-0.09090909090909083 1.0096642401086826
-0.07070707070707061 0.9149167196744973
-0.050505050505050386 0.8149904585811949
-0.030303030303030276 0.8911912817877188
-0.010101010101010055 0.7482676667892594
0.010101010101010166 1.1897490575186858
0.030303030303030498 0.9056735152660633
0.05050505050505061 0.7582628416820897
0.07070707070707072 1.4675396986433764
0.09090909090909105 1.1154917745706467
0.11111111111111116 2.2803636003798076
0.1313131313131315 1.1628383120003922
0.1515151515151516 1.0160951450554574
0.1717171717171717 1.1236354104889867
0.19191919191919204 1.5322731640723288
0.21212121212121215 1.145304101926237
0.2323232323232325 0.9593259993800155
0.2525252525252526 2.160735438968098
0.27272727272727293 1.049396691090573
0.29292929292929304 2.1913168930576616
0.31313131313131315 1.682685252890624
0.3333333333333335 1.2418274831113385
0.3535353535353536 2.373622867698331
0.3737373737373739 1.666093305866498
0.39393939393939403 1.3848597766474662
0.41414141414141437 1.8544466519948946
0.4343434343434345 2.383265164003688
0.4545454545454546 2.1825882359785482
0.4747474747474749 2.2799928678691894
0.49494949494949503 2.6916335195969485
0.5151515151515154 2.11612862411466
0.5353535353535355 2.2210329848716315
0.5555555555555556 2.0207174449107415
0.5757575757575759 1.5696376030735633
0.595959595959596 2.13410532800663
0.6161616161616164 2.8791147545271505
0.6363636363636365 1.5803058214822543
0.6565656565656568 2.8507097669957053
0.6767676767676769 2.4581511830938827
0.696969696969697 2.0297316523689455
0.7171717171717173 2.4605312306459712
0.7373737373737375 3.185276326406841
0.7575757575757578 2.2858982398015972
0.7777777777777779 2.8717930007143866
0.7979797979797982 3.048565185453946
0.8181818181818183 2.2775260373606914
0.8383838383838385 2.9298524215469746
0.8585858585858588 2.9312337782204096
0.8787878787878789 2.5679147934505933
0.8989898989898992 3.0719741637310634
0.9191919191919193 2.6939061642837485
0.9393939393939394 2.6478159049980237
0.9595959595959598 2.425300119538972
0.9797979797979799 3.1137879168962748
1.0 2.82832400301817
进行预测
1
2
3
4
5
6
7
| x_test = 3.21
predict = sess.run(pred, feed_dict = {x:x_test})
print("预测值:%f" %predict)
target = 2 * x_test +1.0
print("目标值:%f" %target)
|
预测值:7.142073
目标值:7.420000
1
2
3
4
|
x_test = 3.21
predict = sess.run(w) * x_test + sess.run(b)
print("预测值:%f" %predict)
|
预测值:7.142073